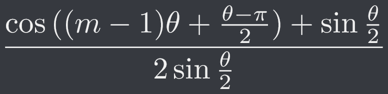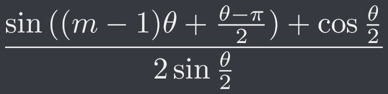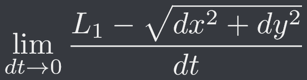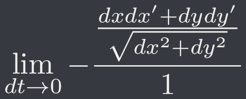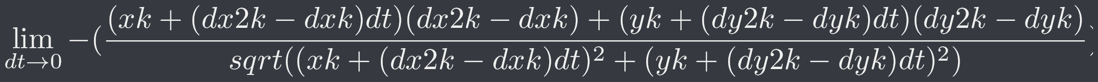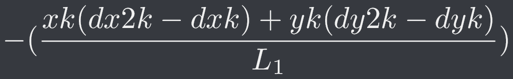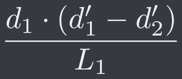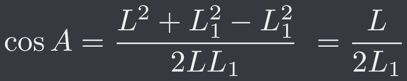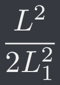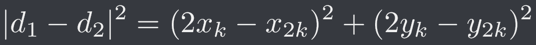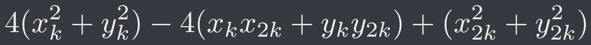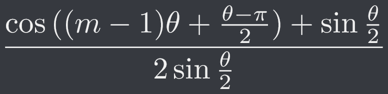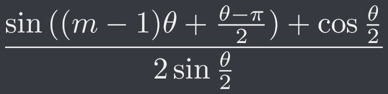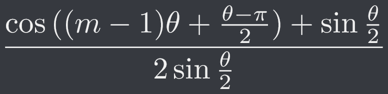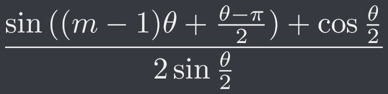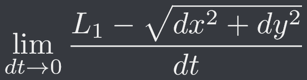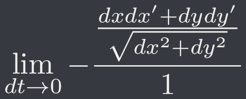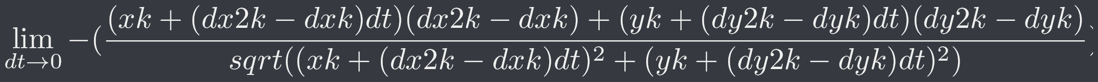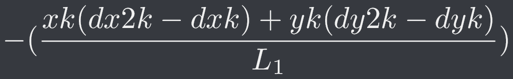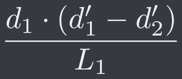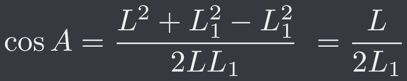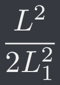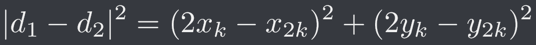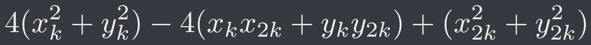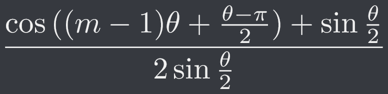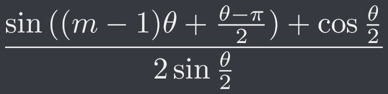題目連結:
題目大意:
輸入有多筆測試資料,每筆佔一列。每列給定兩正整數 n 、 k(3 ≦ n ≦ 500,1 ≦ k < n),代表現在有 n 位 Loki 各自佔據正 n 邊形的一個頂點。
該正 n 邊形的邊長為 1 公尺長,且頂點被順時針編號為 0 ~ n - 1。而編號 i 的 Loki 會去追編號 i + k 的 Loki(當 i + k ≧ n 時,為 i + k - n,即 i + k 模 n 之值)。已知所有 Loki 的速度固定為每秒 1 公尺。
試問多少秒後所有 Loki 會聚集在正 n 邊形的正中心?請將秒數四捨五入至小數點第二位後輸出。
範例輸入:
3 1
3 2
4 1
4 2
4 3
5 1
6 1
7 1
8 1
10 1
20 1
50 1
100 1
200 1
87 86
94 87
89 4
8 7
範例輸出:
0.67
0.67
1.00
0.71
1.00
1.45
2.00
2.66
3.41
5.24
20.43
126.82
506.77
2026.59
383.62
64.55
100.68
3.41
解題思維:
(文極長、大量數學式子、圖多注意。文末有「結論」)
(如果死圖,請先重整。若多次重整或點進圖片都無法解決請通知我)
首先,我們需要將所有 Loki 的位置座標化。
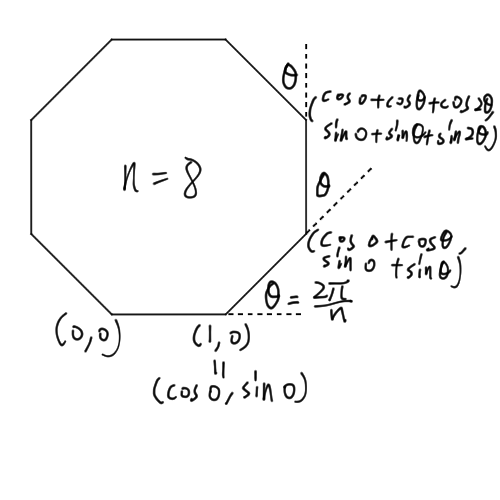
我們可以隨便選擇一個位置定為原點 (0, 0) 然後讓正 n 邊形的一條邊放在 +X 方向上,剩下的部分則往 +Y 方向延伸。可以從下圖 n = 8 的例子
中看到各個點的座標從原點按照逆時針方向依序為
(0, 0)、
(1, 0) 同時也是 (cos 0, sin 0)、
(cos 0 + cos θ, sin 0 + sin θ)、
(cos 0 + cos θ + cos 2θ, sin 0 + sin θ + sin 2θ)、
……
也就是每個點為前一個點的座標值加上一個偏移量。而該偏移量原本為 (1, 0),每轉一個彎後就會旋轉 θ 弧度。因此如果轉了 q 個彎,偏移量將是 (cos qθ, sin qθ),而其長度維持為 1 單位長。
其中 θ 為正 n 邊形的外角。因為外角總和為 360°(即 2π 弧度),因為如果你從邊上任一個位置出發繞一圈回來,你會發現你恰好「轉了」2π 弧度。因此 θ = 2π ÷ n(因為要轉 n 次彎)。
因此可以看到一個點如果需要從原點按逆時針走 m 條邊才能到,則該點座標 (x, y) 為
x = cos 0 + cos θ + cos 2θ + …… cos (m-1)θ
y = sin 0 + sin θ + sin 2θ + …… sin (m-1)θ
而原點本身會被定義為繞一圈回來後的點,即 m = n。
我們在此定義以上座標系為 P1。
此時我們將這些點重新編號:原點為編號 0,逆時針依序為編號 1 、 2 、…… 、 n - 1。而我們可以想像:當所有 Loki 位於正 n 邊形的中心時,即代表著編號 0 第一次追上了編號 k 的 Loki。
因此我們只要知道編號 0 與編號 k 的 Loki 的相對速度以及一開始的距離,然後將距離除以速度即可得到追上的時間,也就是到達中心的所需時間。而其他對的條件與編號 0 與編號 k 這對相同,所以可以只考慮這對。
而為了知道編號 0 與編號 k 的 Loki 的相對速度,我們同時也需要編號 2k 的 Loki,因此我們需要算出編號 k 和編號 2k 的位置。雖然可以按照上面的式子慢慢地一個點一個點地推得。
而我們也可以利用公式求得點座標,而公式可以參考
這題的作法推得。不過,公式還可以從別的角度推得——我們一樣利用一個正 n 邊形,只是這次原點位於圖形的中心。因此所有點的座標如下圖所示:
其中 r 為頂點到正 n 邊形中心的距離,同時也是正 n 邊形的外接圓半徑。可以看到外接圓同時也是三角形 ABC 的外接圓,因此根據正弦定理(Law of Sines)可得
r = s ÷ (2sin(θ ÷ 2))
其中 s 為正 n 邊形的邊長,在本例中為 s = 1。並且我們將此座標系稱為 P2。
可以看到原先座標系 P1 的原點對應到本座標系 P2 的點 C、編號 1 對應到點 A 、……以此類推。因此可以看到上圖中的紅色線即為原座標系 P1 位於 X 軸上的那條邊。
而我們可以得出該條邊與 X 軸的夾角為 T = (π - θ) ÷ 2 弧度。所以將整個座標順時針旋轉 T 弧度,紅色邊將與 X 軸平行。
因此 P2 座標系原本的每個點
(rcos(Mθ), rsin(Mθ))
現在變為
(rcos(Mθ - T), rsin(Mθ - T))
得新座標系 P2'
可以看到原本座標系 P1 的原點現在位於 P2' 座標系的
(-rsin(θ ÷ 2), -rcos(θ ÷ 2))
因此將整個座標系平移 (rsin(θ ÷ 2), rcos(θ ÷ 2)) 就變回原本的座標系 P1 了。不過此時可以看到 P2' 的點變為
(rcos(Mθ - T) + rsin(θ ÷ 2), rsin(Mθ - T) + rcos(θ ÷ 2))
而 P2' 座標系的 M 之值對應著 P1 座標系的 m - 1。所以我們便證明了
cos 0 + cos θ + cos 2θ + …… cos (m-1)θ
等價於
rcos((m - 1)θ - T) + rsin(θ ÷ 2)
且
sin 0 + sin θ + sin 2θ + …… sin (m-1)θ
等價於
rsin((m - 1)θ - T) + rcos(θ ÷ 2)
因此將 r 、 T 展開後可得 x 座標為
而 y 座標為
回到題目本身,我們需要編號 k 和編號 2k 兩個 Loki 的位置,而它們的座標套用 m = k 和 m = 2k 即可求得。
我們定義編號 k 位於 (xk, yk) 、編號 2k 位於 (x2k, y2k)。
因為編號 0 要追著編號 k,而編號 k 要追著編號 2k。所以兩者各自有著方向向量 d1 = (xk, yk) 和 d2 = (x2k - xk, y2k - yk)。不過如果我們現在放任他們跑剛好一秒(這邊只沿著向量走,沒有跟著 Loki 們的位置變動而變動方向),他們移動到的位置並不是原座標直接加上這兩個向量,因為這兩個向量的長度不一定為 1。
因此我們需要將算出 L1 = sqrt(xk ^ 2 + yk ^ 2) 、 L2 = sqrt((x2k - xk) ^ 2 + (y2k - yk) ^ 2),其中 sqrt() 為取平方根。
然後將 d1 除以 L1 、d2 除以 L2 便可以將兩個向量長度調整為 1。令這兩個向量為
d1' = (dxk, dyk)
d2' = (dx2k, dy2k)
因此現在如果我們放任他們移動 dt 秒(在不做方向更新的情況下),編號 0 、編號 k 的位置將位於
(dxk × dt, dyk × dt)
和
(xk + dx2k × dt, yk + dy2k × dt)
因此 dt 秒後編號 0 與編號 k 的座標差距為
(xk + (dx2k - dxk) × dt, yk + (dy2k - dyk) × dt)
將其命名為
(dx, dy)
因此 dt 秒後它們兩個的距離從 L1 變成了
sqrt(dx ^ 2 + dy ^ 2)
令此值為 d。因此兩者的相對位移為
L1 - sqrt(dx ^ 2 + dy ^ 2)
根據「距離除以時間等於速率」,因此兩者的相對速率為
(L1 - sqrt(dx ^ 2 + dy ^ 2)) ÷ dt
而我們可以看到在任何時刻下,編號 0 與編號 k 的相對速率 v 應維持一定值。因為整個系統是對稱的(每對 Loki 都經歷著相似的移動路徑),所以不管何時(直到抵達中心為止)這些 Loki 都可以形成一個稍微旋轉後縮小版本的正 n 邊形,如下圖 n = 5 、 k = 1 時的示意圖:
(值得注意的是,這只是一個逼近示意圖,與真實情況有所差別)
所以當我們將 dt 盡可能地逼近 0 時,上面的相對速率之值便會收斂於實際的相對速率 v,也就是 v =
但是當我們直接代入 dt = 0 時,會發現分子分母都會是 0,代表其為「0/0」之不定式(Indeterminate Form)。因此可以套用羅必達法則(L'Hôpital's Rule,參見
維基)將分子分母各自對 dt 微分,求得
然後將 dx 、 dy 的定義值代入進去便可以得到相當長的式子(暫時如此),其為
這時可以將上式代入 dt = 0 了,得
可以看到分子為 d1 向量與 (d1' - d2') 這個向量之內積(Dot Product),因此先改寫為
套入內積
其中 d1 的長度恰好就是 L1 且 d1' = d1 ÷ L1 、 d2' = d2 ÷ L2,再加上 L2 實際上等於 L1。因為編號 0 到編號 k 的距離理所當然地應等於編號 k 到編號 2k 的距離。因此可以改寫為
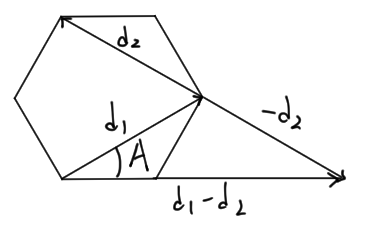
那麼 cosA 呢?其按內積定義為 d1 與 (d1' - d2') 之夾角。而該角度同時也是 d1 、 (-d2) 、 (d1 - d2) 三個向量所形成的三角形中與 d2 相對之角度,如下圖 n = 6 、 k = 2 時的示意圖:
是故,根據餘弦定理(Law of Cosines)可以求出
其中 L 為 (d1 - d2) 這個向量的長度。因此式子便成為了
接著我們要求 L ^ 2 的值,可以看到其值為
將等號右邊展開為
合併一些項次(令 L2k 為原點到 (x2k, y2k) 的距離)且再套用一次內積便改寫為
而角度 α 為 (xk, yk) 、 (x2k, y2k) 以及 d2 這三個向量圍成的三角形中與 d2 相對之角度,且別忘記 d2 的角度恰為 L1。因此再度根據餘弦定理可得
因此 L ^ 2 等價於
也因此我們費盡千辛萬苦終於求得了相對速率 v 的值為
最後,因為編號 0 的 Loki 與編號 k 的 Loki 距離 L1。而我們也已經知道相對速率 v,所以可以推得所有 Loki 位於正 n 邊形的中心所需時間恰為 L1 ÷ v ,即
結論:
編號 k 與編號 2k 的 Loki 相對於編號 0 之座標可以表為
作為其 X 、 Y 座標(代入 m = k 以及 m = 2k 即可)。
而我們將編號 0 與編號 k 的距離定為 L1 、編號 0 與編號 2k 的距離定為 L2k,則抵達中心所需時間為
(2021 / 7 / 27 14:52 更新:作者有在留言區用一句話講解他使用的公式,只用了一句話和一張圖XD)
題外話:
如果有人想到了更精簡的證明過程(等價的公式也行),我強烈地希望可以告訴我。當然如果上述內容有紕漏,哪怕是多小的錯誤都歡迎指正。
本題我花了半天到一天想出解法(實際上是邊調整、邊天馬行空想出來的,總共提交了 27 次的程式碼),而統整成以上的過程則花了整整兩天。很久沒有這麼費神了。
而在觀察的過程中我編寫了一個模擬的程式(
這個。用 python 寫成的,其需要另外安裝 matplotlib 這個模組),可以用來模擬本題的「追逐」。
程式執行前可以調 n(裡面命名為 amount)、 k(裡面為 chase)還有一個角色類似 dt 的 stepLength 這三個變數的值。此程式可以調「模式」,看你是要觀察這 n 個點在每個時刻所形成的正 n 邊形之樣式(mode = "SHAPE")、還是要追尋這 n 個點的移動軌跡(mode = "TRACE")。
除了會畫圖以外,它還會顯示根據 stepLength 而得出的逼近之抵達時間 nowTime(到中心的一個範圍內便算做抵達)。
有興趣或是想要更進一步觀察本問題的可以參考上面的鏈結一下。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。