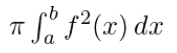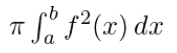題目連結:
題目大意:
輸入第一列給定一正整數 t (1 ≦ t ≦ 100),代表有 t 筆測試資料,每筆佔三列。
測資第一列給定一非負整數 n (0 ≦ n ≦ 5),代表有一多項式 f(x) 之最高次方為 n 次。
測資第二列給定 n + 1 個整數(介於 -10 ~ 10 之間),代表 f(x) 的最高次方項次到最低次方項次之係數,其中最高項次之係數必不為 0。
測資最後一列給定兩整數 a 、 b (-10 ≦ a ≦ b ≦ 10),代表取值的左右端點(即從 x = a 到 x = b)。
試問,f(x) 以標準座標平面之 X 軸為軸心旋轉一圈所形成之物體之體積(從左端點到右端點的範圍中)為何?即是問,f(x) 沿 X 軸之旋轉體(參見
維基頁面)體積為何?
範例輸入:
範例輸入 #1
3
0
1
-4 -2
0
9
-1 4
0
3
-3 10
範例輸入 #2
3
1
-5 -4
9 10
1
-10 2
-10 5
1
-8 0
-4 4
範例輸入 #3
3
5
-8 0 -8 0 -6 7
4 5
2
2 8 3
0 1
3
5 8 4 9
-10 -1
範例輸出:
範例輸出 #1
6.28
1272.35
367.57
範例輸出 #2
8338.83
122710.61
8578.64
範例輸出 #3
895239610.20
210.91
75795399.04
解題思維:
從題目大意給定的維基鏈結可以看到,f(x) 沿著 X 軸之旋轉體體積為
上式可以解釋為,對於每個極短區間 x ~ x + dx,該區間所形成的「截片」之體積,因為區間長度 dx 極小,所以體積之值逼近於截面面積之值。而截面面積為 π(r ^ 2),其中 r 為 f(x)。將所有的切片的「體積」加起來即是整個旋轉體脂體積。
如果對微積分(Calculus)的基本觀念不甚熟悉,推薦可以參見 3Blue1Brown 的《微積分的本質》(The Essence of Calculus)的系列,以下為第一集
首先 f(x) 的項次輸入就不贅述(直接用陣列存即可,但是記得輸入是從高項次開始給),接著我們求出 (f(x)) ^ 2 ,可以參見一般的多項式相乘(如
此題)。
然後求出 (f(x)) ^ 2 做不定積分後所形成的多項式 F(x),其中 f(x) 每一項 Cx ^ i 之項次積分後會變為 (C ÷ (i + 1))x ^ (i + 1)。
之後求出 F(b) - F(a) ,最後再將這個差值 × π 即是所求。
此次分享到此為止,如有任何更加簡潔的想法或是有說明不清楚之地方,也煩請各位大大撥冗討論。