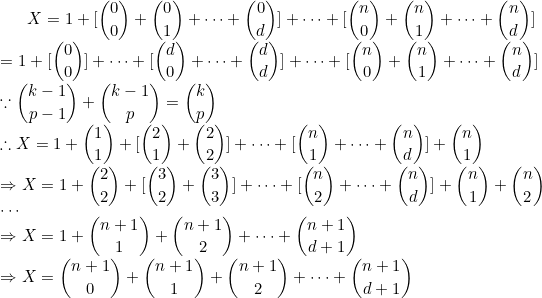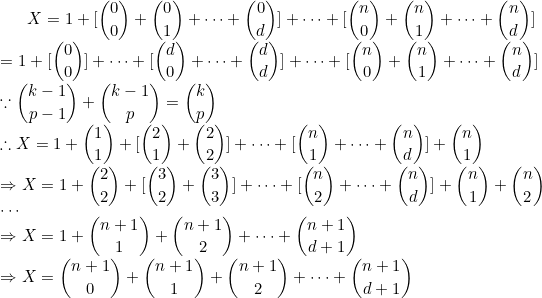題目連結：
題目大意：
在一維空間中，切一刀能使空間變兩個，切 n 刀最多可以使空間變為 n ＋ 1 個；二維空間中，一刀兩個、兩刀最多四個、三刀最多七個……
第一列給定一正整數 N （1 ≦ N ≦ 10 ^ 4），代表有 N 個測試資料，每筆佔一列。每列給定兩正整數 D 、 C （1 ≦ D 、 C ≦ 50），依序代表要切割的維度以及切割的次數。試問在 D 維下，切 C 刀最多可以使該空間分成幾個子空間？
範例輸入：
範例輸入一：
4
1 1
1 2
2 2
1 3
範例輸入二：
6
2 1
2 2
2 3
3 1
3 2
3 3
範例輸出：
範例輸出一：
2
3
4
4
範例輸出二：
2
4
7
2
4
8
解題思維：
這個問題屬於幾何學以及組合學上，直譯稱為超平面的安排、擺放（Arrangement of hyperplanes）。二維的超平面是一般的直線、三維則是平面、四維以上通稱超平面。
一維情況很直觀，每多切一刀，區域最多可以加一。因此 n 刀，區域數為 n + 1 。而其他維度以上的開始變得複雜，但是我們可以這麼想：
令 Ad,k 為 d 維下 k 個超平面的最佳擺放方式，使得子區域數 r(Ad,k) 為最大。
隨便考慮 k 個中的其中一個超平面 P，則 r(Ad,k) ＝ r(Ad,k-1) + (P 新切出來的子區域數)。
而因為 Ad,k 是最佳的擺放方式之一，所以超平面 P 會與其它 k - 1 個超平面一定會有交會（否則就可以與原先沒有交會到的相交，產生更多的子區域），如下圖二維的情況：
紅線與其它四條黑線交於四個「點」。根據一維的情況，超平面為「點」。因為有四個點，所以空間被分為 4 + 1 ＝ 5 個。因此紅線通過了 5 個子區域，也因此將這 5 個子區域再一分為二。所以該紅線考慮進來後，子區域的數目 + 5 。
所以當 d 維的超平面與其他 k - 1 個 d 維超平面相交時，其相交的情況為 k - 1 個 d - 1 維的超平面。所以情況會降為那 k - 1 個 d - 1 維超平面的排列情況。因此， r(Ad,k) ＝ r(Ad,k-1) + r(Ad-1,k-1)。
所以r(Ad,k) ＝ r(Φ) + r(Ad-1,0) + r(Ad-1,1) + …… + r(Ad-1,k-1) ，其中 Φ 代表沒有超平面的情況，所以 r(Φ) ＝ 1。
在二維且有 n 條線的情況下：
r(A2,n) ＝ 1 + r(A1,0) + r(A1,1) + …… + r(A1,n-1) ＝ 1 + 1 + 2 + …… + n
＝1 + n + n(n - 1) ÷ 2 ＝ (n, 0) + (n, 1) + (n, 2) ，其中 (n, k) 代表 n 個物品取 k 個出來的方法數，即 n! ÷ ((n-k)! × k!)。
可以看到 d + 1 維並有 n + 1 個超平面的情況下，r(Ad+1,n+1) 為下列算式的值：
而其值等價於
證明如下：
較直觀的證明如下（利用巴斯卡三角形與組合數的關係）：
目標是說明所有方框的數字總和 + 1 為圓框內的數字之和。先看右邊一系列黑色的線，我們將由上至下數的第三層的 1 拉到第四層，然後 3 + 1 ＝ 4 、6 + 4 ＝ 10 、 10 + 10 ＝ 20，所以我們完成了 20 那個圓框。同樣地，灰色（較深的那個灰色）那一系列下來我們得到 15 、淺灰得到了 6 。最後再加上 1 便得到了所有圓框的數字。
而上面不僅限於此，任何維度 d 、任意數量 n 的超平面，都可以畫成類似於上面的圖。並得到類似的約化結果。
因此，我們得到了在 d 維的情況下切 c 次所擁有的最多的子區域數量為
(c, 0) + (c, 1) + …… + (c, d)
此次分享到此為止，如有任何更加簡潔的想法或是有說明不清楚之地方，也煩請各位大大撥冗討論。
達人
