上一篇提到高次多項式求根時，
若多項式存在有理數解，
則必然可以使用有理根定理。
這一篇，
敝人就是要跟大家分享有理根定理的思考邏輯。
當然，
還是不會證明。
對於一個一元多項式，
習慣上我們會把它展開寫成：
的形式。
我們會把所有的項目，
包括常數項都歸納在等號的左邊，
讓等號右邊為0，
這樣我們就能透過因式分解的方式把等號左邊變成一個連乘積的形式：
這麼多個(qx-p)當中，
只有當其中的某一項是0的時候才能令等號成立對吧？
因此x只要滿足任何一個能讓(qx-p)為0的數值，
那此時的x就是這個多項式的解（或者說是根）。
因為對於n次多項式而言，
我們最後一定會分解成n個(qx-p)形式的數值去連乘，
因此一個n次多項式就必然會有n個解，
如果解的數量少於n個，
那只是因為包含「重解」（某兩個或多個解完全相同）或「複數解」（帶虛數的解）的關係。
回到主題，
對連乘當中的某一項(qx-p)，
如果我們令這一項等於0，
那麼x是多少？
聰明的你一定不假思索就能回答：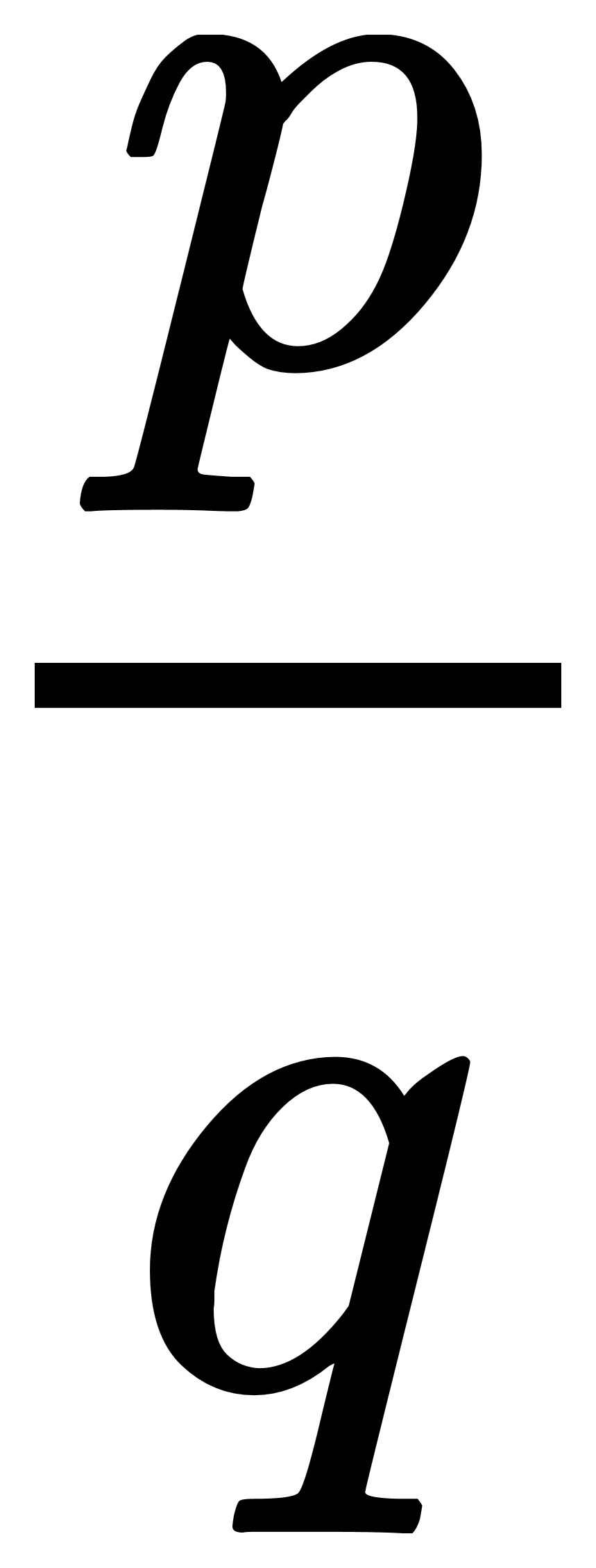
我們回頭看看並比較這兩個多項式的表達形式：
跟
當中最高次項的係數a0，
是不是正是q0、q1…qn的乘積呢？
必然是的吧？
多項式因式展開的過程中能達到最高次項的就只有所有帶x的項互乘而已不是嗎？
同理，
常數項an，
也必然是p0、p1…pn的乘積對吧？
只有常數乘以常數才會是常數，
不然就會帶有變數了不是嗎？
因此，
對任何一個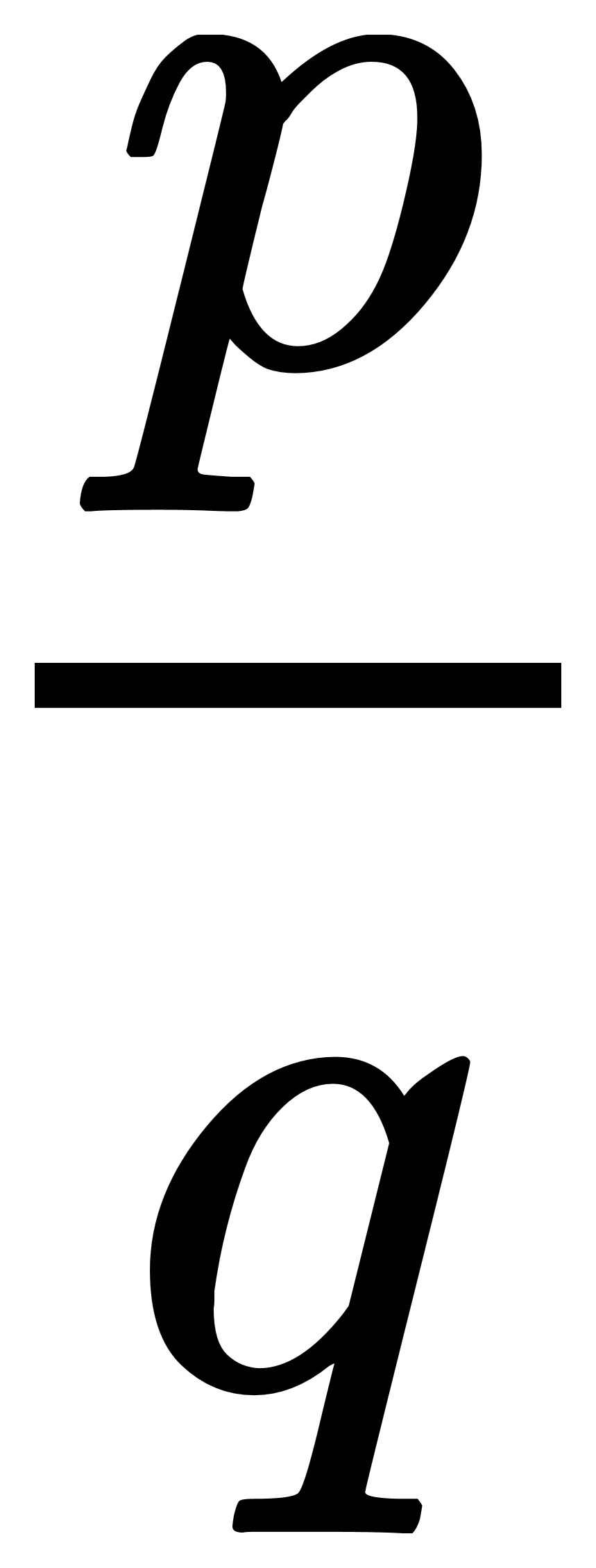形式的有理數解，
形式的有理數解，p一定是常數項的因數，
而q也一定是最高次項係數的因數，
這就是「有理根定理」的核心。
但回到問題的開頭，
有理數的定義是什麼呢？
有理數Q的定義是，
Q一定可以寫成兩個互質整數的比。
例如整數4是有理數，
因為整數4等於
，
，4跟1互質而且都是整數。
又或者小數-2.6是有理數，
因為它等於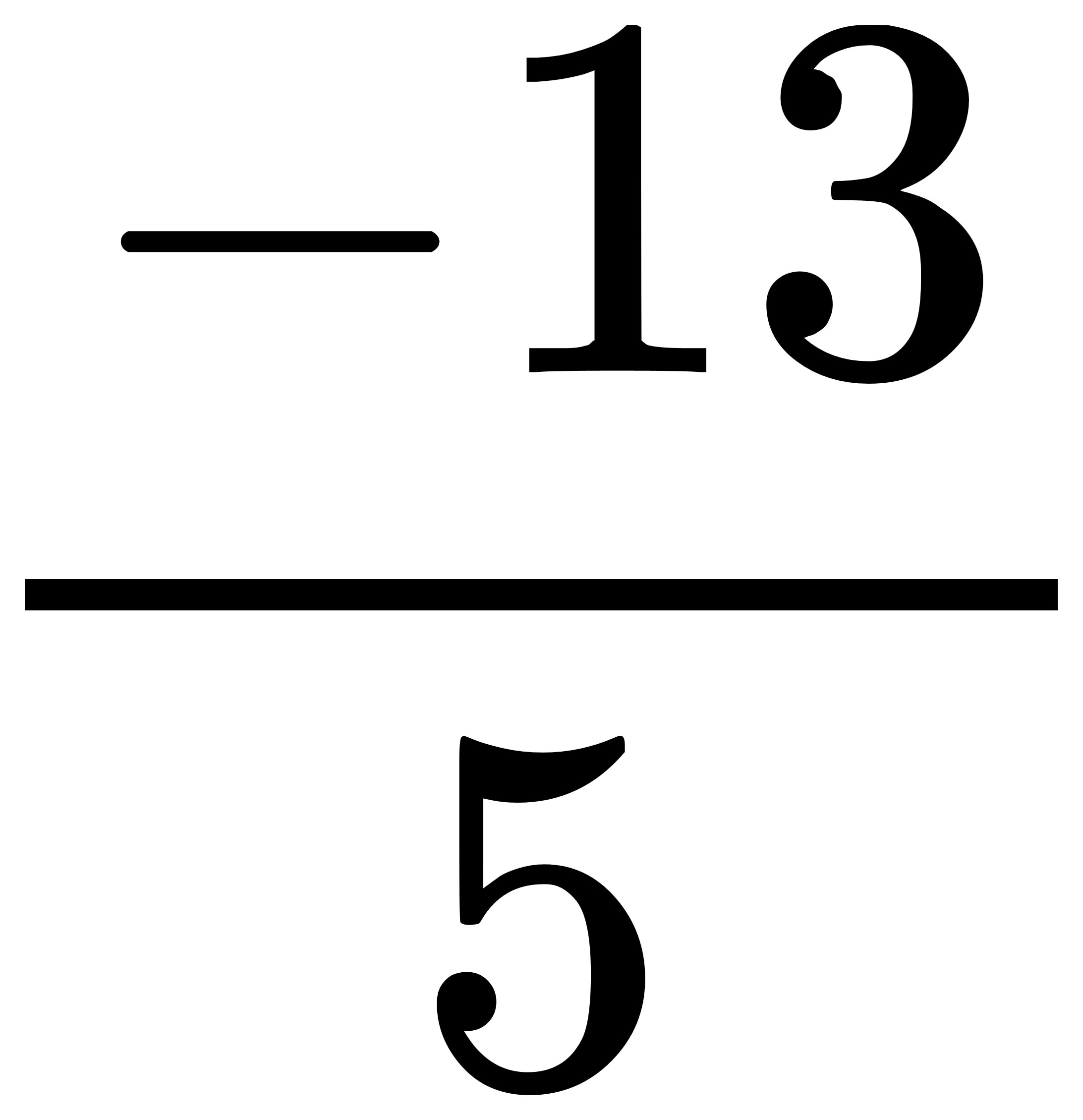
，
，5跟-13也都是整數且互質。
甚至循環小數42.857142 (857142循環)也是有理數，
因為它等於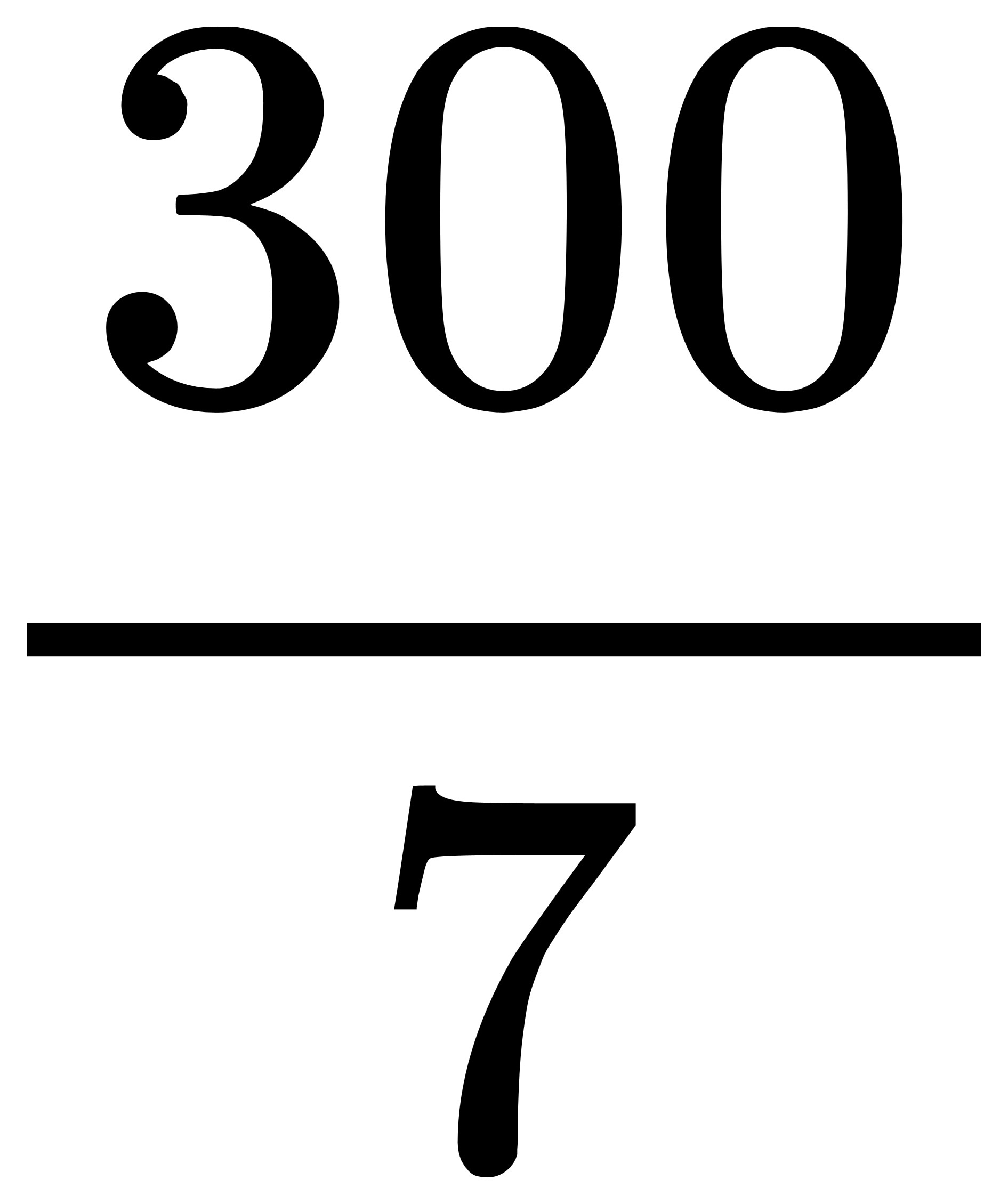
。
。因此我們令某一項(qx-p)=0來求有理數根，
前提就是p、q都是整數且互質，
那麼萬一這個多項式包含無理數根甚至虛根的話，
是否有理根定理就不成立了呢？
例如，
上一篇提到的例題就包含了2個虛根，
為什麼有理數定理依然成立呢？
這就是接下來要解說的部分，
也是這篇為什麼存在的理由。
首先，
無理數根就是泛指所有無法找到任何一組整數p、q並寫成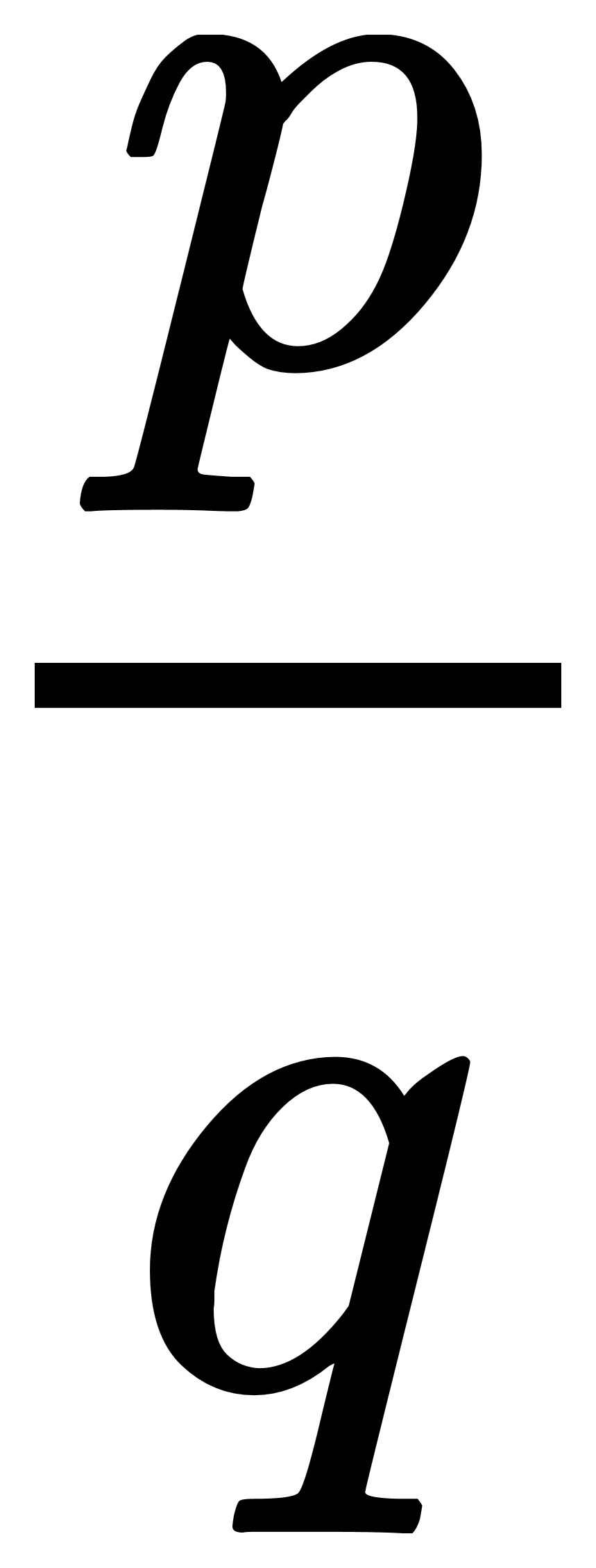形式的根，
形式的根，又或者說無理數根的p或q當中必然包含無理數，
這樣那組根才會是無理數。
那麼，
我們說，
一組多項式必然可以寫成所有根的連乘形式，
如果當中包含無理根，
也就是某一項根中的(qx-p)包含無理數會發生什麼情況呢？
答案是：係數一定會出現無理數。
舉例來說，
假設某個3項式的解是4、根號2、根號3，
那它就一定可以寫成這個形式：
如果把它展開會變成什麼情況？
會變成：
係數上包含了一大堆無理數，
但很明顯的，常數項確實是三個解的乘積對吧？
那麼是不是我們把可以被常數項整除的某個整數找出來是否就能找到解呢？
當然可以，
只是通常來說遇到這種題目我們會無從下手，
因為到底怎樣算整除這點我們就會卡死了。
怎麼說？
這題明顯看起來有4這個根只是巧合，
但為什麼2根號2不能是解？
2根號2也可以被常數項漂亮地除開啊。
我們只知道根可以被常數項除開，
但可以被除開的數有無限多個，
我們又該如何下筆去試？
下筆的標準在哪？
這是說不清楚的，所以原理雖然可理解，
但面對係數帶無理數的多項式，
基本上就不用想利用有理根定裡去尋找有理數解了。
因此，
我們可以肯定地說：
要運用有理根定理找有理根必須包含2個條件：
1、所有項目的係數必須都是整數
2、必須包含有理數解，如果沒有有理數解，那麼當然是找不出答案的囉！
第一點好判斷，
如果有理數必然可以寫成兩個整數的分數形式，
那麼我們只要乘以分母，
就必然可以把多項式化成每一項的係數都是整數的形式，
因此實際上只要不包含無理數或複數形式的係數就符合條件一，
因此在判斷上不會太困難。
而第二項則是說，
在這個形式下，
把最高次項的係數根常數項分別做因數分解，
然後排列組合每一個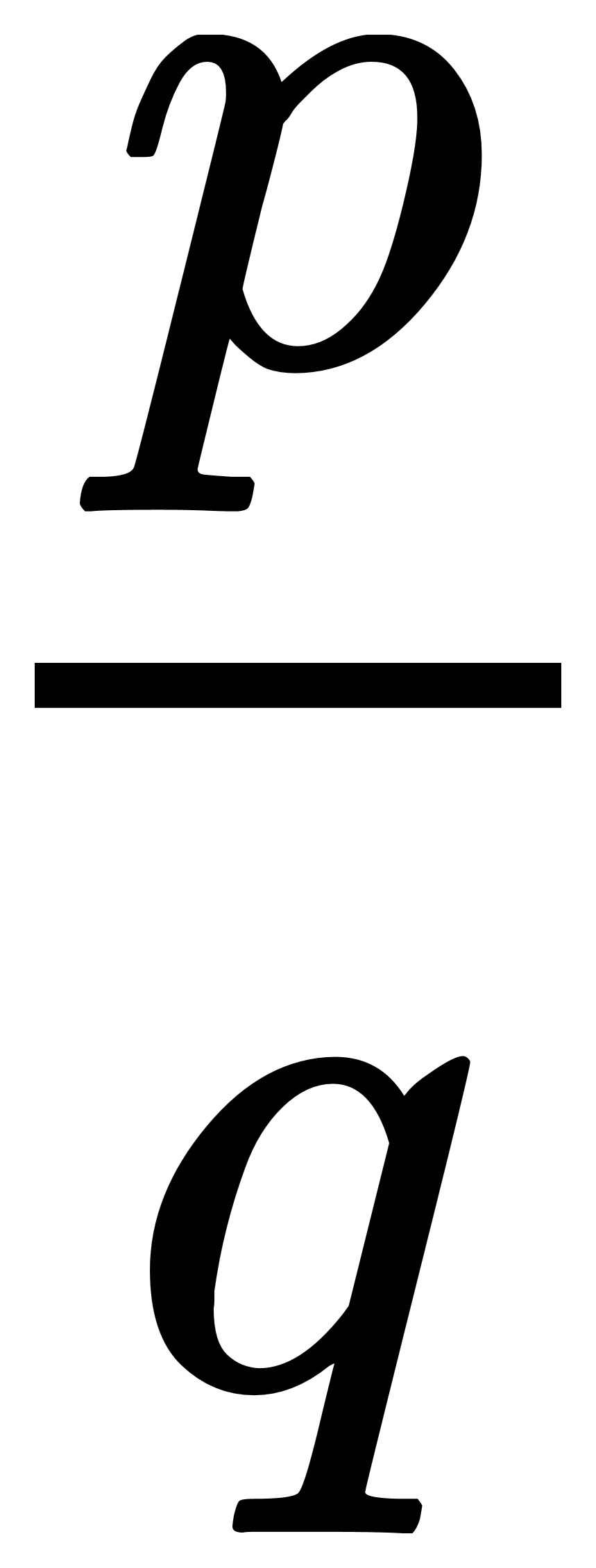代回元多項式去求解，
代回元多項式去求解，若成立就代表找到一組解，
若所有組合都不成立那就代表此多項式沒有有理數解了。
到此為止，
解釋了有理根定理的基本要求，
就是所有項的係數都須為有理數。
但是為什麼包含無理根甚至複數根的多項式，
也能利用有理根定理呢？
這是因為，
這些多項式的無理根或複數根屬於特殊形式，
它的結構會剛好使它在乘開的過程中，
複數或無理數的部分會剛好彼此削掉，
只留下有理數的部分。
國中我們學過一個公式：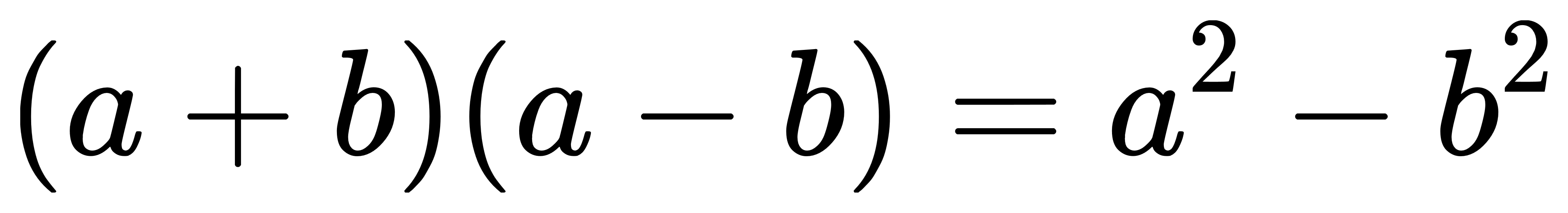
注意到沒有？
如果今天a、b的部分是無理數或複數也無妨，
反正乘起來的結果不會讓a、b單獨存在而是只會留下彼此的平方，
因此只要平方是有理數就沒問題了對吧？
因此對於以下兩種形式的解，
我們依舊能保證係數全都是有理數：
當中a、b、c均為有理數且i是虛數單位。
對於這兩種形式的無理根或複數根，
就必然能保證所有的無理數（或虛數）項會在展開的過程中削掉，
只留下有理數係數的項。
提問：
開三次方根或任意次方的方程式也會具有這個形式的解嗎？
例如x三次方=-8之類的。
這點當然囉。
x三次方等於-8，
就會寫成：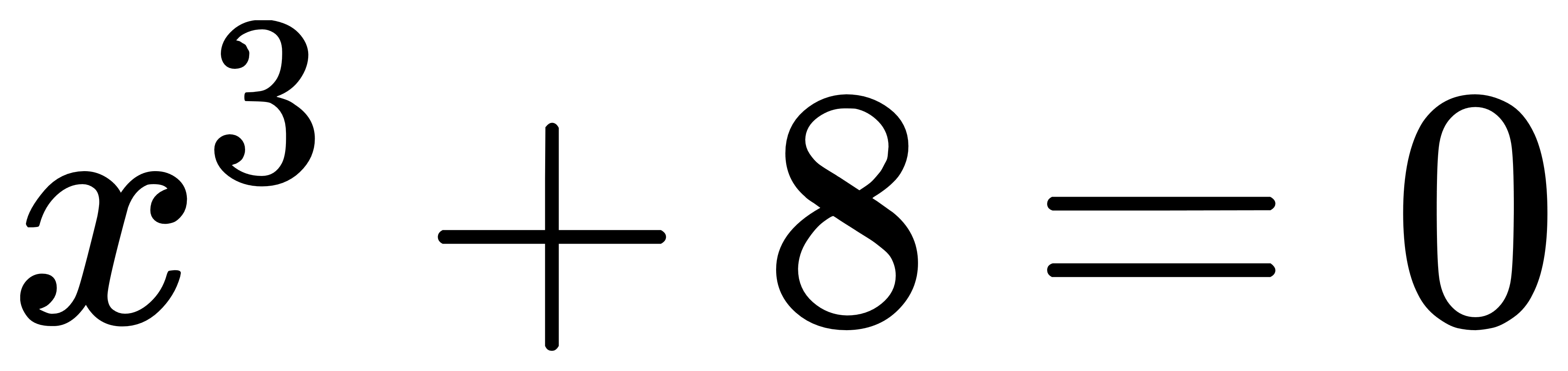
既然沒有無理數根複數項，
那當然就能使用有理根定理來找根。
8的因數只有1、2、4、8，
搭配正負號也就8個，
很快地我們找到了-2的一個根，
因此我們可以確定(x+2)是這個多項式的一個因式。
利用長除法分解多項式，
我們可以把這個多項式寫成這樣：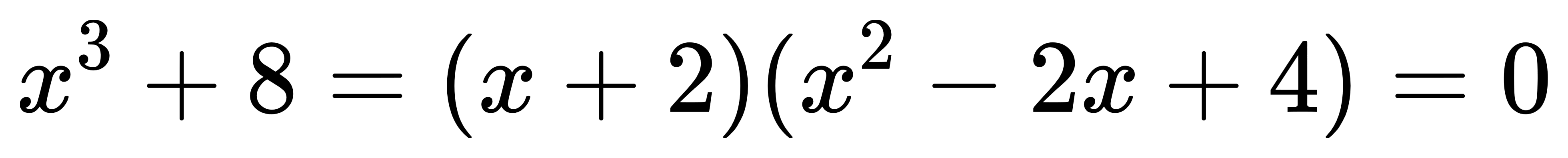
因此我們只要對後面的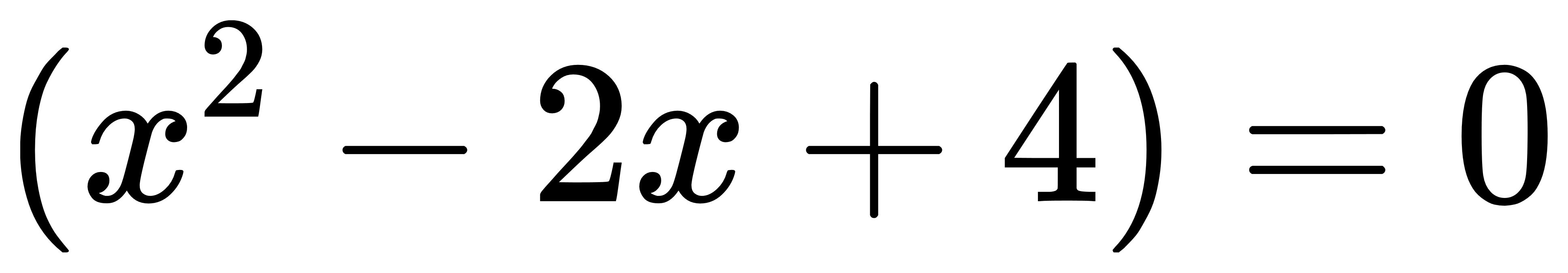
去做求解即可，
去做求解即可，而二次多項式的根有公式解：
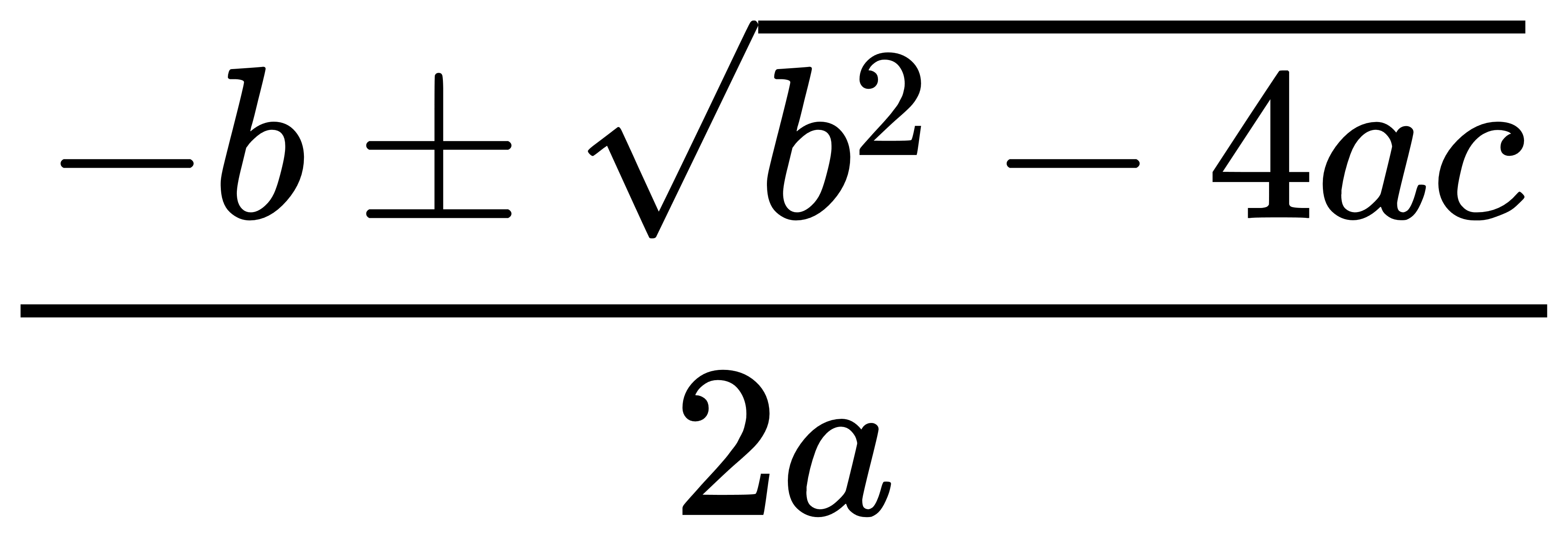
以這題的解來說，
求出來的另外兩組根為虛根：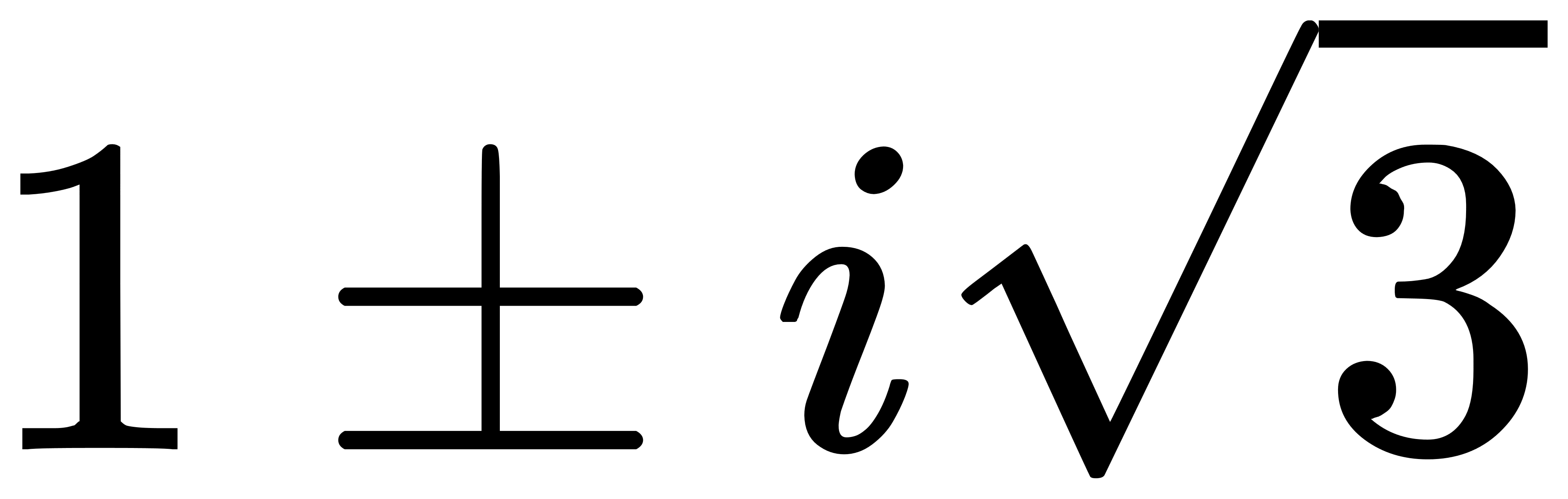
不信？
帶回驗算看看：
（請務必記得：
）
）
確實滿足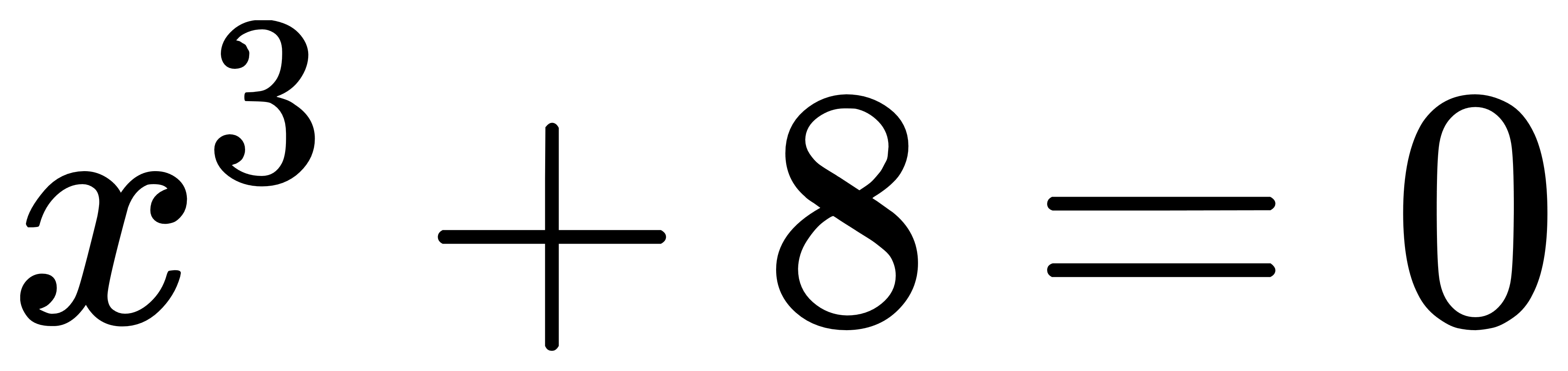沒錯吧。
沒錯吧。一個平方根複數的3次方竟然會是一個整數，
有沒有感到非常意外呢？
這就是數學神奇的地方。
以上就是對有理根定裡的一些細節補充，
抱歉這篇文章也許對許多人來說過於艱澀，
但如果你對中學數學有興趣的話，
那還希望你會喜歡。
